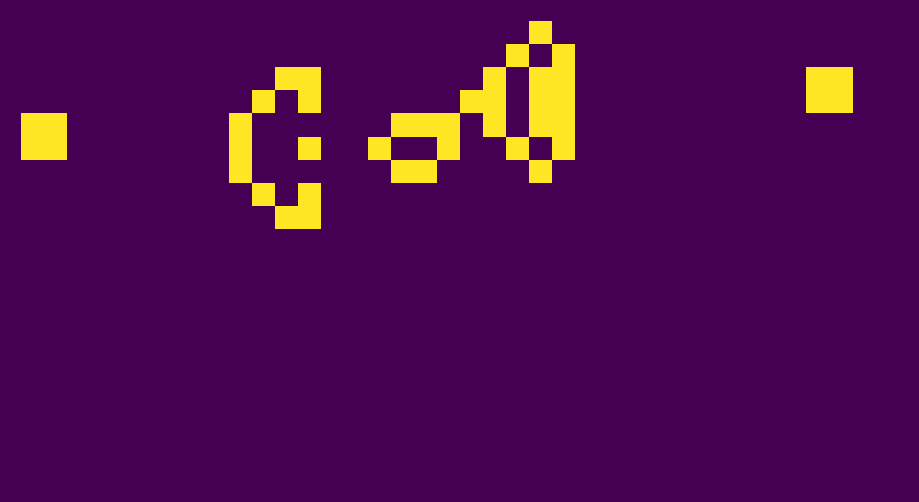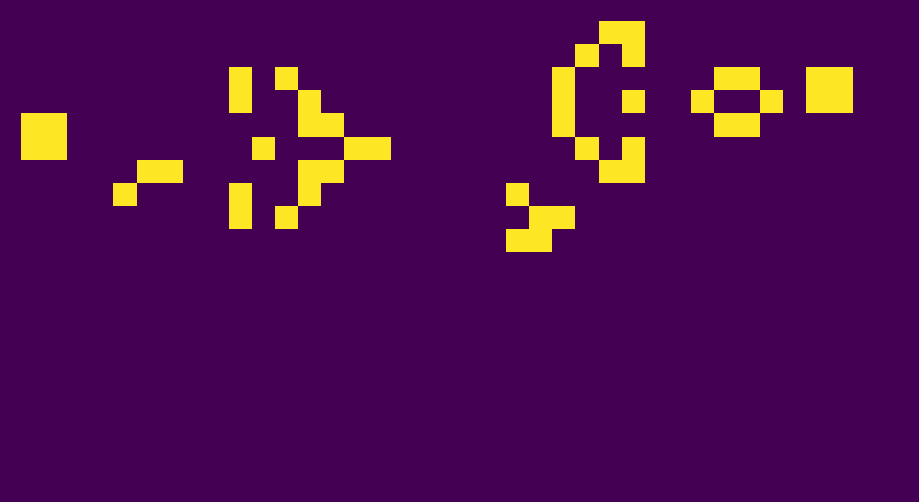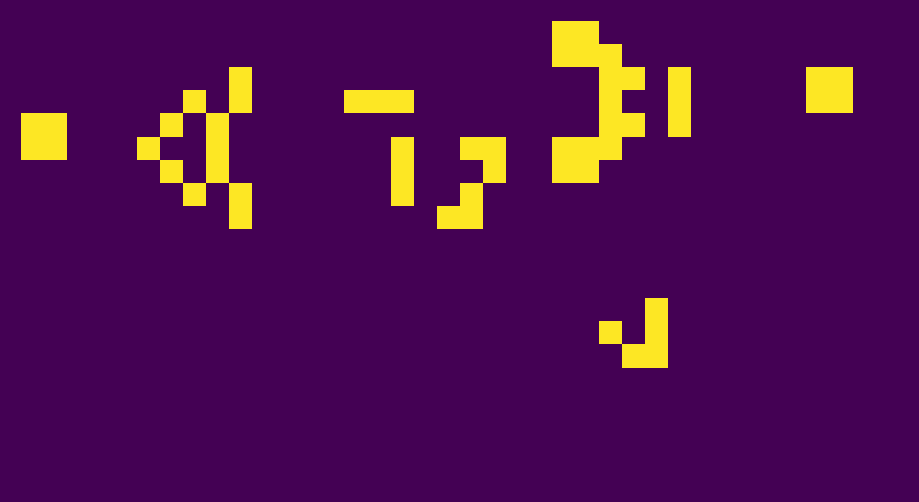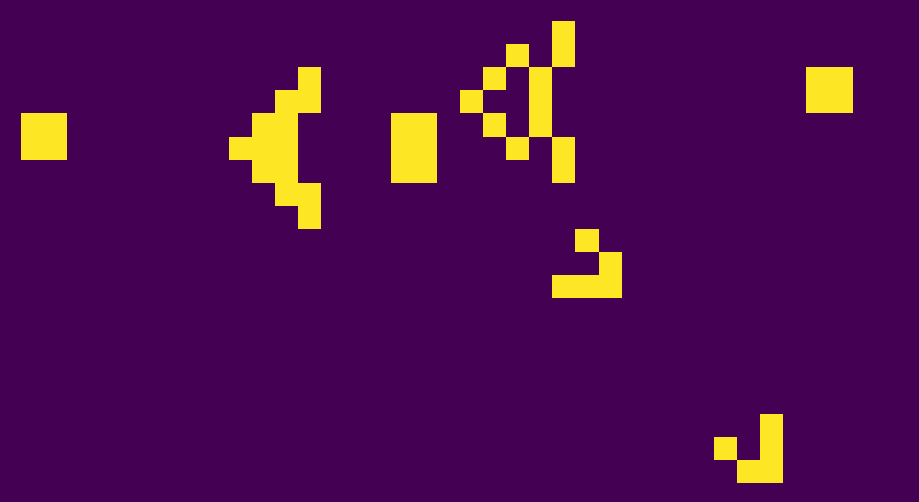The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970. It is a zero-player game, meaning that its evolution is determined by its initial state, requiring no further input. One interacts with the Game of Life by creating an initial configuration and observing how it evolves. It is Turing complete and can simulate a universal constructor or any other Turing machine.
Rules
The universe of the Game of Life is an infinite, two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, live or dead, (or populated and unpopulated, respectively). Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:
- Any live cell with two or three live neighbours survives.
- Any dead cell with three live neighbours becomes a live cell.
- All other live cells die in the next generation. Similarly, all other dead cells stay dead.
Examples of patterns
Many different types of patterns occur in the Game of Life, which are classified according to their behaviour. Common pattern types include: still lifes, which do not change from one generation to the next; oscillators, which return to their initial state after a finite number of generations; and spaceships, which translate themselves across the grid.
Still Lifes
| Block |
Beehive |
Loaf |
Boat |
Tub |
 |
 |
 |
 |
 |
Oscillators
| Blinker |
Toad |
Beacon |
Pulsar |
 |
 |
 |
 |
Spaceships
| Glider |
Light Weight Spaceship |
Middle Weight Spaceship |
Heavy Weight Spaceship |
 |
 |
 |
 |
Glider Gun
| Gosper Glider Gun |
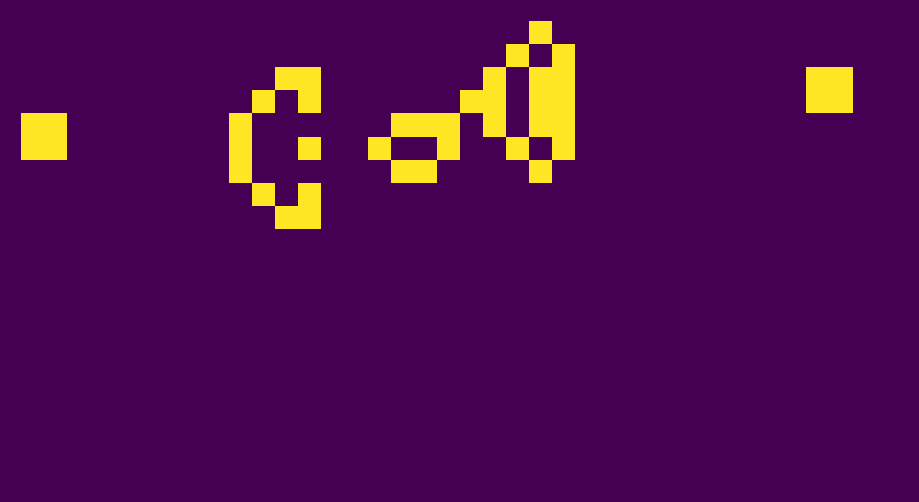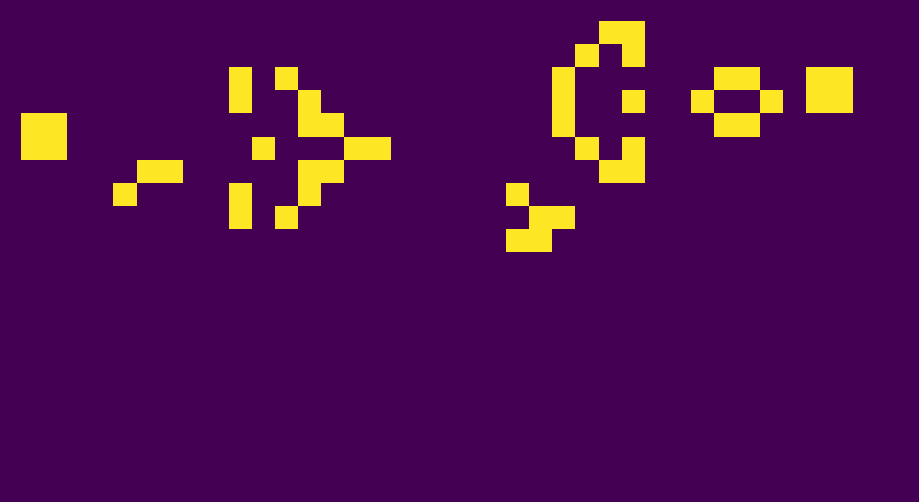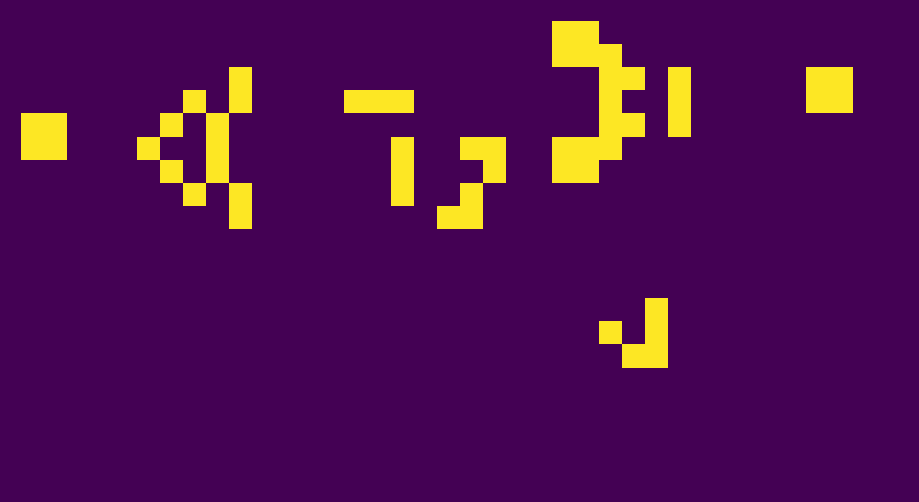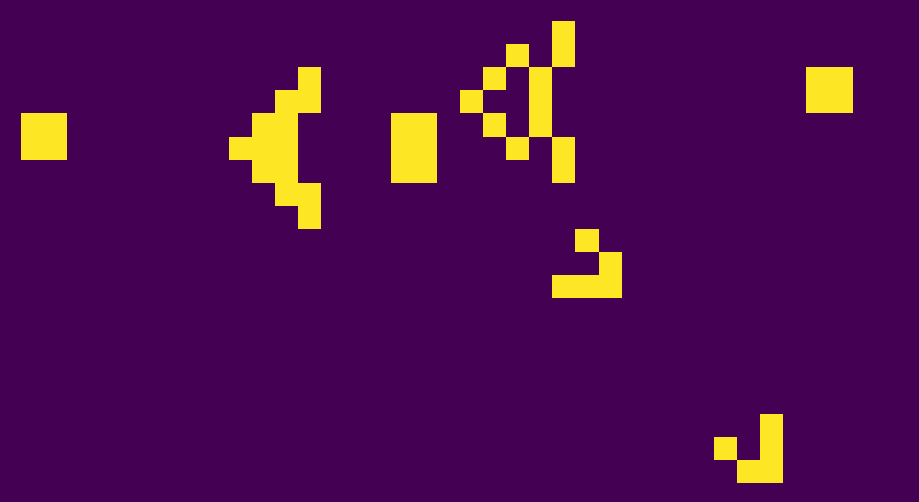 |
References
- Wikipedia
- Scholarpedia
- Code of above patterns are available in this repository. You can try simulating by changing values but this may be better.
-
Game of Life simulated by Game of Life, Watch here